
Identifying high-risk factors for diseases while preserving privacy
Machine learning algorithms are widely used to improve health care, for example to identify risk factors for diseases. These algorithms require a lot of data, often divided over different sources. In practice, combining these data sources is both legally and technically challenging.
When scientific researchers want to use personal medical data for machine learning algorithms in the European Union, they need to comply with the General Data Protection Regulation (GDPR). Local data can often be used for scientific research purposes, however it becomes challenging when data from different sources needs to be combined. This is because, first of all, the GDPR aims at using as little data as possible, while machine learning thrives on large datasets. Secondly, consent from patients is typically needed, and acquiring this consent is time-consuming and causes practical problems, for example because the hospital is no longer in contact with the patients.
This is where our solution comes in. This blog explains a solution for training a machine-learning algorithm using Secure Multi-Party Computation (MPC). MPC is a set of cryptographic techniques that allows several different parties to jointly compute on data, just as if they had a shared database. Cryptographic techniques are used to protect the data, so that it can be analysed in a way that prevents the parties involved from ever being able to access the data of other parties.
Although no real patient data was used, the set-up of the proposed MPC solution is inspired by the following real-life situation. In Rotterdam, there is a group of patients that both is insured by insurance company Zilveren Kruis and took part in a program by hospital Erasmus MC. On one side, Erasmus MC has data on the lifestyle of these patients, for example their exercising behaviour. On the other side, Zilveren Kruis has data on different attributes such as number of hospitalization days and healthcare usage outside the hospital. These datasets, once combined, could be used to train a prediction model, for example to predict the number of hospitalization days of a patient. However, concerns about privacy and consent (to name a few) mean that these parties cannot simply put their data together to allow for a straightforward analysis.
In 2018 TNO, together with Erasmus MC and Zilveren Kruis, started a pilot within the H2020 Project BigMedilytics to develop a secure algorithm to predict the number of hospitalization days for heart failure patients. Note that only synthetic data was used during this MPC set-up. We focus on securely training the algorithm, with a prediction model as output; see Figure 1 for a simplified example.
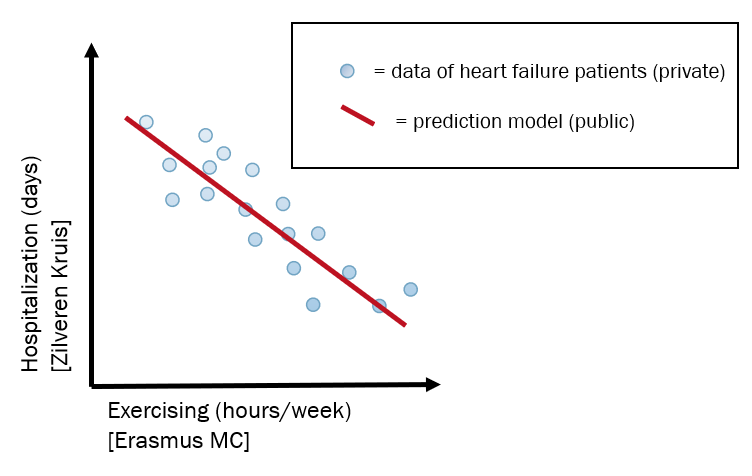
Figure 1: A simplified example of the data involved. Zilveren Kruis and Erasmus MC have data on the same patients (blue dots), but the former only on hospitalization days and the latter only on exercising. The data cannot be combined as in this picture, but with the MPC solution, the prediction model (red line) can be calculated.
Once the algorithm is trained, the resulting coefficients (simplified as the red line in Figure 1) are revealed to the participating parties. These results can be used in a non-encrypted way for applying the model on a single patient, or to get scientific insights into the disease.
Our solution involves three parties; Zilveren Kruis, Erasmus MC and ZorgTTP. Only the first two parties have data and in theory they do not need a third party. However, healthcare intermediation company ZorgTTP is also involved in the protocol on request of both parties. Technically this has an advantage, because the involvement of the third party makes the implementation faster; furthermore, the secure regression protocol that we use requires at least three parties.
Our solution consists of two phases. It starts with a Secure Inner Join, that is needed in preparation of the second phase; the Secure Lasso Regression.
Secure Inner Join
In the set-up, Zilveren Kruis and Erasmus MC both have synthetic data on non-existing patients. A group of patients are present in both data sources, but the attributes of both datasets are different (e.g. hospitalization days at Zilveren Kruis and exercise at Erasmus MC). We say these datasets are vertically partitioned. We call inner join the combination of the identifiers that are represented in both datasets, together with their attributes. For example, in Figure 2, the inner join consists of patients B and C and their attributes.
A first challenge lies in determining the inner join in such a way that the parties involved do not learn which patients are in the inner join. At the same time we want it to be possible to train a secure machine learning model on the data. To this end, we developed a Secure Inner Join protocol. The input of this protocol consists of both datasets from Zilveren Kruis and Erasmus MC, the output is an encrypted version of the combined database, which contains the associated attributes of the patients that are in both initial datasets.
In the Secure Inner Join protocol patients are matched by an identifier (ID, based on birth date and postal code). Both parties use a keyed hash to encrypt the IDs and homomorphically encrypt their attributes and send this encrypted data to ZorgTTP (see step 1 and 2 in Figure 2). Homomorphic encryption is a form of encryption that enables performing computations on the encrypted data without first decrypting it. A keyed hash is comparable to a fingerprint and enables ZorgTTP to match the hashed IDs without seeing the original IDs (step 3).
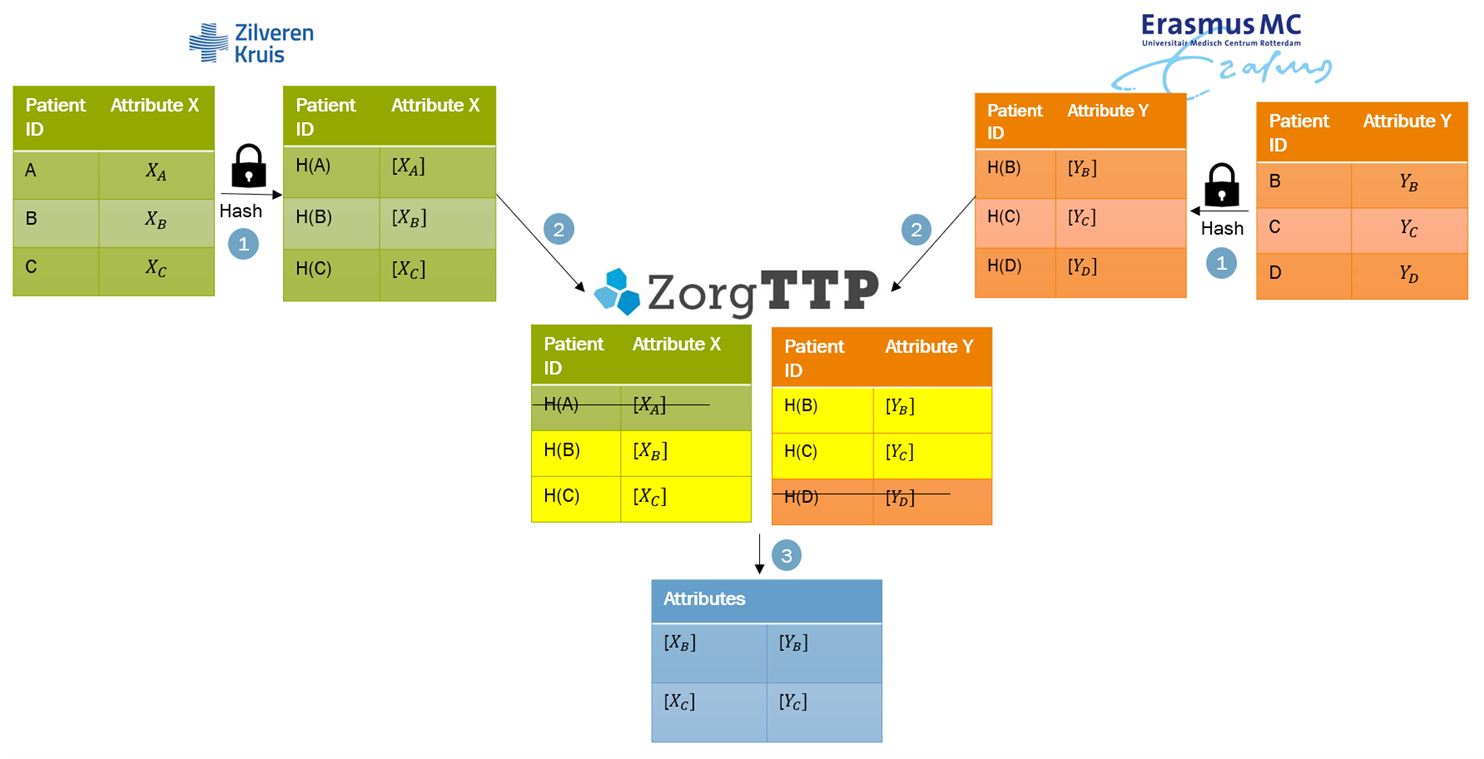
Figure 2: Secure Inner Join protocol. If a value A is hashed, this is denoted by H(A) and if a value X is encrypted it is denoted by [X].
Once the intersection is determined, an interactive protocol takes place to convert the encrypted inner join into “shares”, obtained with a form of distributed encryption known as secret sharing. Secret sharing is an cryptographic technique where a secret value (in this case an element in the inner join) is distributed among the (in this case three) parties, so that they can perform computation on the value without actually knowing it. After the Secure Inner Join, we ended up with the right input, namely the secret-shared data, for the Secure Lasso Regression.
The TNO MPC Secure Inner Join is publicly available and provides functionality to join two vertically partitioned databases with the help of a third party, where not of the involved parties learns the data of the any other party.
The TNO MPC Communication Module is publicly available and provides communication between MPC nodes using HTTP(s).
Secure Lasso Regression
Once the intersection with all attributes is secret-shared, the secure regression can start. In this project the Lasso (Least Absolute Shrinkage and Selection Operator) regression was implemented using the MPyC framework, a Python library for MPC based on secret sharing. We chose Lasso regression because this method results in a sparse model with few coefficients; some coefficients can become zero and are eliminated from the model. Therefore the Lasso regression allows for minimizing the number of features that have an impact on the model, thus meeting the proportionality and data-minimization requirements for subsequent non-encrypted application of the model to identify high-risk patients.
The input of the secure regression is the secret-shared inner join of both datasets, as we ended up with in the previous paragraph. A secret-shared database allows for calculation on secret values. We implemented all calculations on the secret shares necessary for Lasso Regression in MPyC. The optimal coefficients are found by a Gradient Descent (GD) algorithm, an iterative optimization algorithm. The secure version of the GD algorithm can also be used as a building block on which different predicting algorithms can be build, such as the classification model Support Vector Machine.
After performing these calculations, we end up with a secret-shared result of the regression, namely the coefficients of the prediction model. This result can be revealed by bringing together these secret shares. Note that we only reveal the coefficients, while the input data is still secret-shared and is therefore kept private.
Zilveren Kruis and Erasmus MC receive the final output of the secure regression, which consists of the plaintext coefficients of the regression, trained on their combined synthetic input data (simplified as the red line in Figure 1). In a real-life setup, the result of this protocol would be that if the hospital wants to predict the expected risk of hospitalization of a new patient, they only need the data of this one patient to apply the prediction model and perform the prediction. More general, insight is gained in which factors play a role in the disease, as was analysed on a large combined dataset.
The TNO MPC Secure Lasso Regression is publicly available and provides functionality to perform lasso regression with three or more parties using (secure) gradient descent.
Results/ Status
In July 2020, TNO ran the demo of the described set-up with synthetic data of Zilveren Kruis and Erasmus MC, and with ZorgTTP as a helper party. See Figure 3 for a screenshot of the demo. Every party was equipped with a Linux VM, which communicated with the VMs of the other parties over the internet, with connections secured with TLS. We tested the performance and scalability of our solution using artificial data, by measuring the running time and complexity of various phases of the protocol. In figure 4 you can see the performance results. Performing the secure regression on a dataset with 10.000 patients and 10 features takes a bit over half an hour.

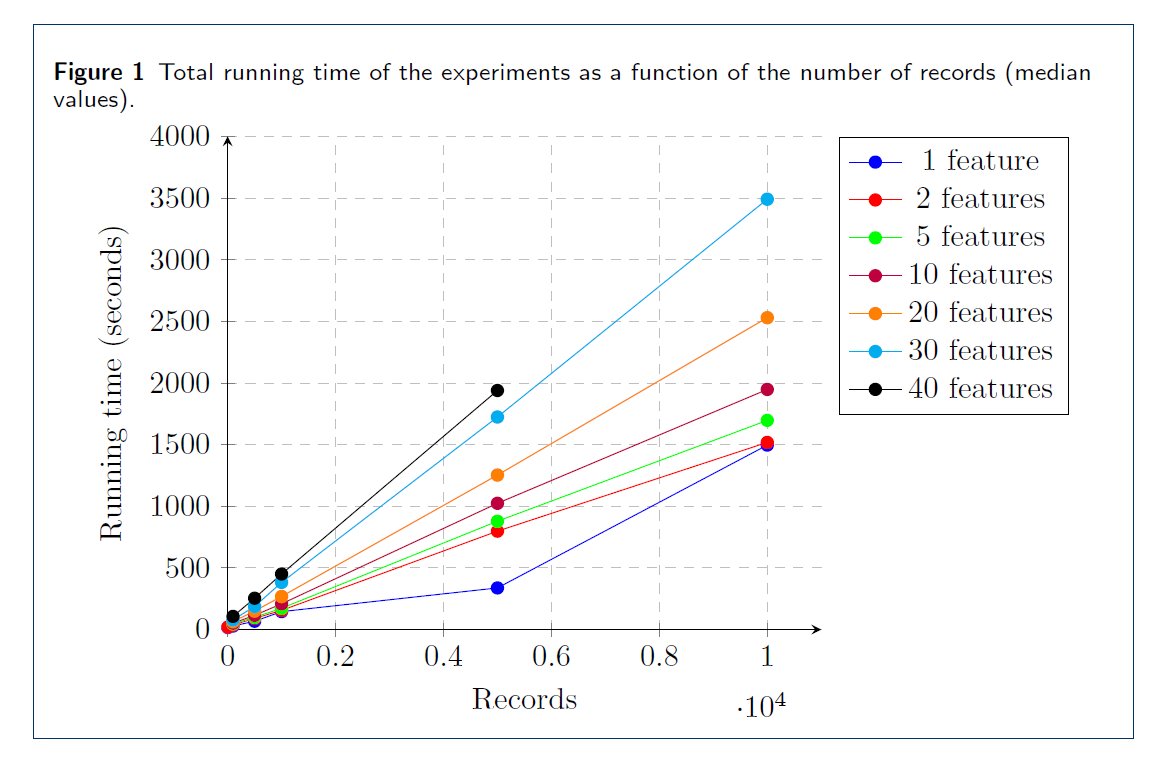
Figure 4: Performance results. Records are the number of patients in the inner join, features are attributes. One can read from this picture that performing the secure regression on a dataset with 10.000 patients and 10 features takes a bit over half an hour.
Conclusion
MPC has the potential to ease the current complicated process of data coupling. It can contribute to GDPR principles such as data minimization when combining data. The mathematical guarantees for the patients’ privacy ensures accurate prediction models without sacrificing privacy. Therefore the application of MPC will allow more data to be used, and will hence lead to more trustworthy results, while safeguarding the privacy of involved individuals.
Altogether, the results of our demo are promising. With fake data, we showed that a Lasso regression on 10.000 patients with 10 features can run within half an hour. In the future, it will be essential to investigate which hurdles need to be overcome within organisations to start using MPC, including legal and compliance aspects. We are confident that such steps will result in more MPC pilots with real medical data in the near future.
This blog is an update of The Sugar Beet: Applied MPC blog and explains how privacy enhancing technology can benefit the research on high risk factors for a disease.
The BigMedilytics project has received funding from the European Union’s Horizon 2020 research and innovation program under grant agreement No 780495.

